Adding Plausible and Implausible gives us a very rich and powerful notion of indeterminacy, which is a simple extension to Generative Analysis four-valued logic that incorporates intuition in a useful way. Note, however, that this extension is informal—we do not add the new states of Plausible and Implausible to the Proposition state machine in the Generative Analysis metamodel (Figure 4). This is why the terms are not written in the Literate Modeling font.
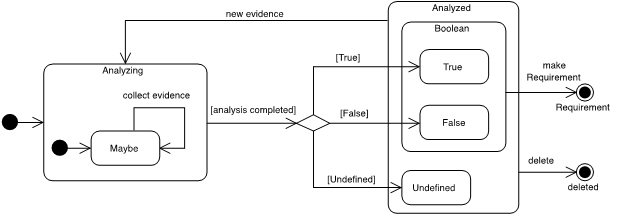
Figure 4: We do not add Plausible and Implausible to the Proposition state machine.
Click to open full-sized image
In fact, we could easily formalize the informal states, Plausible and Implausible and incorporate them into the Proposition state machine but we choose not to do so because in practice they are insufficiently well-defined. In Generative Analysis it is important that all Propositions in the system are in one of the states Maybe, True, False, or Undefined because these states are clearly defined based on the evidence. The informal states of Plausible and Implausible, however, are based on intuitions, which, as we saw above, are very different from and operate orthogonally to evidence. Thus, while they are very useful states for the modeler to work with conceptually, they are not useful for the Generative Analysis metamodel because they don't capture concrete information as evidence, just a feeling. Furthermore, while we can expect modelers to agree on True, False, Maybe, or Undefined based on specific, objective evidence, intuition is largely subjective and provides no such basis for agreement. It does, however, provide a good basis for discussion.
A key feature of this informal six-valued logic is that Implausible doesn't distinguish between "likely False" and "likely Undefined". Implausible just means "likely not True". In some cases, we might have a very specific intuition that a Proposition is False or a very specific intuition that it is Undefined, but this amounts to a difference that doesn't make a difference to the analysis activity, so we have never found it useful to make the distinction explicit or capture it. Having the intuition that a Proposition is "likely not True" seems to be good enough to get the analysis job done.
Adding the concepts of Plausible and Implausible does several things:
- Promotes intuition to a first-class analysis activity, which is what it should be. We must take our intuitions seriously, and having notions of Plausible and Implausible allows us to do this in a structured way.
- Allows us to recognise and note intuitions for further investigation. You can do this by adding informal notes (labelled Plausible or Implausible) to the UML model elements or to the database of Propositions. You can even use different colors for Plausible and Implausible.
- Can surface presuppositions and biases. It is very important to uncover these as early as possible because they can skew the analysis activity.
- Provides a direction for the analysis. If, for example, you consider a Proposition to be Plausible, this indicates that you expect to find some supporting evidence, so that is what you should look for first. On the other hand, if you think a Proposition is Implausible, you should first look for contrary evidence. This can provide a useful shortcut in the analysis activity, allowing you to get to the heart of the matter quicker.
Note that Maybe means to keep a completely open mind about something. This can be difficult, because such indeterminism creates a state of cognitive dissonance that many people find uncomfortable. Thus, Plausible and Implausible tend to act as attractors that pull away from Maybe, correctly or incorrectly, as a reflex mechanism to resolve the dissonance. It can be quite hard, and requires practice, to keep a question completely open (Maybe) without having an opinion about it. This drift away from Maybe is something to be very aware of because it can mislead you. One of the Generative Analysis principles is, "Trust no one", so we always analyze our intuitions and look for evidence to validate or invalidate them.
In terms of the software engineering process, working with intuitions in Generative Analysis is straightforward:
- Expect, look out for, and recognise your intuitions.
- Capture them as new Propositions (if they are not already about existing Propositions) if you can. Otherwise, make a note of them somewhere, perhaps on the UML model.
- Categorize them as Plausible or Implausible.
- Analyze them by asking yourself why you think they are Plausible or Implausible and look for specific evidence to resolve them to True, False, or Undefined.
You can apply this process anywhere in the project lifecycle whenever you recognise an intuition, but it tends to have the most impact earlier on in the Inception and Elaboration phases.
We would like to thank John Quinn, Jim's ex-boss at British Airways, for the notions of "plausible" and "implausible" applied to software engineering. John would often look at some model and say that it was plausible or implausible based on his intuitions. And that would trigger the analysis and "the game would be afoot".
