How to incorporate intuition in Generative Analysis
The authors of Generative Analysis: The Power of Generative AI for Object-Oriented Software Engineering with UML define "intuition" and discuss how it operates in relation to propositions and evidence in software engineering models.
In this article, we are going to demonstrate how to incorporate intuition into the logical framework of Generative Analysis in a simple way that is informal, yet very useful.
First, we need to agree on what we mean by "intuition", and because Generative Analysis makes heavy use of Generative AI, let's ask Microsoft Copilot to define intuition for us:
Copilot: Intuition is the ability to understand or know something immediately based on your feelings rather than facts. It's that inner sense that guides you without needing conscious reasoning. For instance, when faced with a decision, trusting your intuition might lead you in the right direction, even when there's no clear evidence. It's like a quiet whisper from your instincts, nudging you toward a choice or understanding that transcends logical analysis. So, next time you have a hunch or a gut feeling, pay attention—it might just be your intuition at work!
That's a pretty good definition, however, we would change "...understand or know something..." to "...feel like you understand or know something...". It is important to distinguish between intuition, which is a feeling that you know something, and actual knowledge, which is based on evidence. Intuition is sometimes right, sometimes wrong, and sometimes not applicable (i.e., not even wrong!) and must not be confused with knowledge, which in Generative Analysis, must be supported by evidence.
Intuition is often overlooked by Software Engineers and others because it is thought to be "unscientific" and/or "untrustworthy". Also, it is generally not a formal part of the software engineering process. This is a shame, because if you have done any job for a considerable time, and thereby gained a lot of experience, then you will certainly have important and useful intuitions, or "gut feelings", about how things work in that domain. These intuitions can, if analyzed objectively, lead you to important knowledge, answers to questions, and solutions to problems. If not analyzed objectively (just accepted or rejected), they can lead to dead ends and wasted time, and if they are not even recognised, they can lead to presuppositions and biases that may be damaging to the project.
For example, having spent many years object modelling, Jim can look at a UML model, and, almost straight away, get a gut feeling for what is right and what is wrong about it, and how it might be improved. These intuitions are based on a lot of largely unconscious processing that his brain performs based on having seen and analyzed so many of these things before. We suppose it is a kind of pattern recognition. Intuitions, however, are not allowed to constrain work on the model in any way until they have been analyzed. Jim's intuitions often turn out to be accurate, and, even if they are not accurate, they generally indicate important avenues for investigation. Even intuitions that might be inapplicable because they are unrelated to the issue at hand can provide sources of creative insight when analyzed.
Incorporating intuition into Generative Analysis is surprisingly simple. As you will know if you have read our book Generative Analysis, the Generative Analysis technique is predicated on a simple four-valued logic, where, as well as the usual True and False values, we also have Maybe and Undefined. Note that from this point, I will use the Literate Modeling convention of using a special font (sic) to indicate terms that refer directly to elements in the Generative Analysis metamodel described in our book.
In Generative Analysis, statements about the system under analysis are captured as Propositions. These are defined as follows:
Proposition: a statement about the system or problem domain that can have one of the following four truth values:
- True – there is evidence to support the truth of the Proposition.
- False – there is evidence to support the falsehood of the Proposition.
- Maybe – there is insufficient evidence to decide on truth or falsehood of the Proposition, but the evidence may yet be discovered.
- Undefined – the Proposition is ill-formed and undecidable. The evidence is contradictory, or no evidence could be found one way or the other.
Figure 1 shows how a Proposition in the state Maybe is, by way of an Analysis activity that accumulates evidence, transitioned to one of the states: True, False, or Undefined. This is the core activity of Generative Analysis&mdash the resolution of indeterminacy through analysis to generate new information.
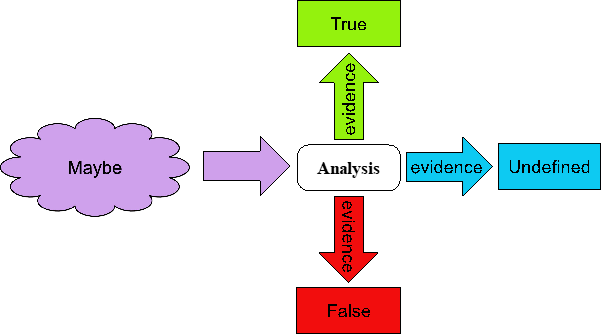
Figure 1: The possible states of a Proposition in Generative Analysis.
Click to open full-sized image
