From the author of
From the author of
From the author of
We can accommodate intuition very easily by extending our four-valued logic to a six-valued logic, where a Proposition can be Maybe, Plausible, Implausible, True, False, or Undefined. Notice that we have not used the Literate Modeling font for the two new states, Plausible and Implausible, because, as we will explain shortly, these are informal extensions that we choose not to include in the Generative Analysis metamodel. The informal model for this extension is shown in Figure 2.
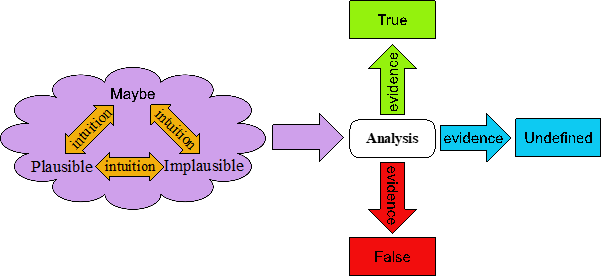
Figure 2: An informal extension to four-valued logic allows for the incorporation of intuition.
Click to open full-sized image
As you can see, while a Proposition is Maybe, we can apply our intuition to say that it is Maybe, Plausible, or Implausible. These states are defined as follows:
- Maybe (as above) – there is insufficient evidence to decide on truth or falsehood of the Proposition, but the evidence may yet be discovered.
- Plausible – there is insufficient evidence to decide on truth or falsehood of the Proposition, but my intuition suggests that it is likely to be True.
- Implausible – there is insufficient evidence to decide on truth or falsehood of the Proposition, but my intuition suggests that it is likely to be not True (i.e., False or Undefined).
Intuition is not the same as evidence, and, in fact, we may say it operates orthogonally to evidence. Figure 3 shows that you proceed from Maybe to True or False by accumulating evidence one way or the other. Intuition operates on a different axis, orthogonal to the evidence axis, where it indicates that a Proposition is Plausible (likely True) or Implausible (likely not True). The Proposition state Undefined is not on either axis, because, by definition, it is neither True, False, Plausible, nor Implausible. We like to think of it existing in a shadowy third dimension lurking below the plane of the page.
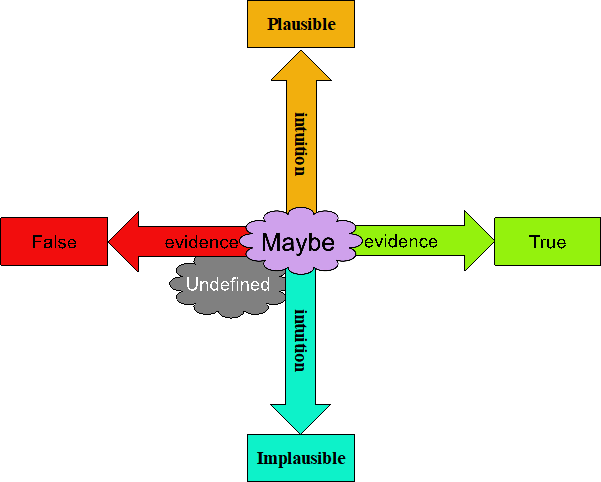
Figure 3: Intuition operates orthogonally to evidence.
Click to open full-sized image