Introduction
This chapter is from the book
This chapter is from the book
This chapter is from the book
The goal of this chapter is to provide a motivation for and an introduction to process control and instrumentation. After studying this chapter, the reader, given a process, should be able to
Determine possible control objectives, input variables (manipulated and disturbance) and output variables (measured and unmeasured), and constraints (hard or soft), as well as classify the process as continuous, batch, or semicontinuous.
Assess the importance of process control from safety, environmental, and economic points of view.
Sketch a process instrumentation and control diagram.
Draw a simplified control block diagram.
Understand the basic ideas of feedback and feedforward control.
Understand basic sensors (measurement devices) and actuators (manipulated inputs).
Begin to develop intuition about characteristic timescales of dynamic behavior.
Describe simple control loops associated with physiological systems.
The major sections of this chapter are as follows:
1.1 Introduction
1.2 Instrumentation
1.3 Process Models and Dynamic Behavior
1.4 Redundancy and Operability
1.5 Industrial IoT and Smart Manufacturing
1.6 Control Textbooks
1.7 A Look Ahead
1.8 Summary
1.1 Introduction
Process engineers are often responsible for the operation of chemical processes. As these processes become larger in scale and/or more complex, the role of process automation becomes increasingly important. The primary objective of this textbook is to teach process engineers how to design and tune controllers for the automated operation of chemical processes.
A conceptual process block diagram for a chemical process is shown in Figure 1–1. Notice that inputs are classified as either manipulated or disturbance, and the outputs are classified as measured or unmeasured in Figure 1–1a. To automate the operation of a process, it is important to use measurements of process outputs or disturbance inputs to make decisions about the proper values of manipulated inputs. This is the purpose of the controller shown in Figure 1–1b; the measurement and control signals are shown as dashed lines. These initial concepts probably seem very vague or abstract at this point. Do not worry, because we present a number of examples in this chapter to clarify these ideas.
)
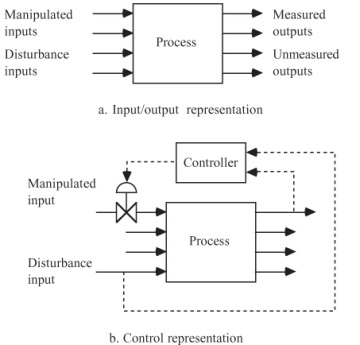
Figure 1–1 Conceptual process input/output block diagram
The development of a control strategy consists of formulating or identifying the following:
Control objective(s)
Input variables
Output variables
Constraints
Operating characteristics
Safety, environmental, and economic considerations
Control structure
We discuss in more detail the steps in formulating a control problem:
The first step for developing a control strategy is to formulate the control objective(s). A chemical-process operating unit often consists of several unit operations. The control of an operating unit is generally reduced to considering the control of each unit operation separately. Even so, each unit operation may have multiple, sometimes conflicting objectives, so the development of control objectives is not a trivial problem.
Input variables can be classified as manipulated or disturbance variables. A manipulated input is one that can be adjusted by the control system (or process operator). A disturbance input is a variable that affects the process outputs but that cannot be adjusted by the control system. Inputs may change continuously or at discrete intervals of time.
Output variables can be classified as measured or unmeasured variables. Measurements may be made continuously or at discrete intervals of time.
All processes have certain operating constraints, which are classified as hard or soft. An example of a hard constraint is a minimum or maximum flow rate—a valve operates between the extremes of fully closed or fully open. An example of a soft constraint is a product composition—it may be desirable to specify a composition between certain values to sell a product, but it is possible to violate this specification without posing a safety or environmental hazard.
Operating characteristics are usually classified as continuous, batch, or semicontinuous (semibatch). Continuous processes operate for long periods of time under relatively constant operating conditions before being shut down for cleaning, catalyst regeneration, and so forth. For example, some processes in the oil-refining industry operate for 18 months between shutdowns. Batch processes are dynamic in nature—that is, they generally operate for a short period of time, and the operating conditions may vary quite a bit during that time. Example batch processes include beer or wine fermentation, as well as many specialty chemical processes. For a batch reactor, an initial charge is made to the reactor, and conditions (temperature, pressure) are varied to produce a desired product at the end of the batch time. A typical semibatch process may have an initial charge to the reactor, but feed components may be added to the reactor during the course of the batch run.
Another important consideration is the dominant timescale of a process. For continuous processes, this is very often related to the residence time of the vessel. For example, a vessel with a liquid volume of 100 liters and a flow rate of 10 liters/minute would have a residence time of 10 minutes; that is, on average, an element of fluid is retained in the vessel for 10 minutes.
Safety, environmental, and economic considerations are all very important. In a sense, economics is the ultimate driving force—an unsafe or environmentally hazardous process will ultimately cost more to operate because of fines paid, insurance costs, and so forth. In many industries (petroleum refining, for example), it is important to minimize energy costs while producing products that meet certain specifications. Better process automation and control allows processes to operate closer to optimum conditions and to produce products where variability specifications are satisfied.
The concept of failsafe is always important in the selection of instrumentation. For example, a control valve needs an energy source to move the valve stem and change the flow; most often, this is a pneumatic signal (usually 3–15 psig). If the signal is lost, then the valve stem will go to the 3-psig limit. If the valve is air-to-open, then the loss of instrument air will cause the valve to close; this is known as a fail-closed valve. If, on the other hand, a valve is air-to-close, when instrument air is lost, the valve will go to its fully open state; this is known as a fail-open valve. These concepts are illustrated in Figure 1–2.
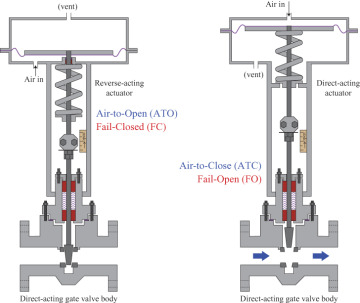
Figure 1–2 Fail-closed and fail-open valves. The fail-closed valve (left) has instrument air entering below the actuator, whereas the fail-open valve (right) has instrument air entering above the actuator. In each case, the loss of instrument air will cause the valve to move in the direction forced by the spring attached to the actuator. Source: GlobalSpec, s.v. How can we change the action of a control valve? Response by tonykuphaldt, September 2011, http://cr4.globalspec.com/thread/75751/How-Can-We-Change-the-Action-of-a-Control-Valve.
The two standard control types are feedforward and feedback. A feedforward controller measures the disturbance variable and sends this value to a controller, which adjusts the manipulated variable. A feedback control system measures the output variable, compares that value to the desired output value, and uses this information to adjust the manipulated variable. For the first part of this book, we emphasize feedback control of single-input (manipulated) and single-output (measured) systems. Determining the feedback control structure for these systems consists of deciding which manipulated variable will be adjusted to control which measured variable. The desired value of the measured process output is called the setpoint.
)
A particularly important concept used in control system design is process gain. The process gain is the sensitivity of a process output to a change in the process input. If an increase in a process input leads to an increase in the process output, it is known as a positive gain. Conversely, if an increase in the process input leads to a decrease in the process output, it is known as a negative gain. The magnitude of the process gain is also important. For example, a change in power (input) of 0.5 kW to a laboratory-scale heater may lead to a fluid temperature (output) change of 10°C; this change is a process gain (change in output/change in input) of 20°C/kW. The same input power change of 0.5 kW to a larger-scale heater may yield an output change of only 0.5°C, corresponding to a process gain of 1°C/kW.
Once the control structure is determined, it is important to decide on the control algorithm. The control algorithm uses measured output variable values (along with desired output values) to change the manipulated input variable. A control algorithm has a number of control parameters, which must be tuned (adjusted) to have acceptable performance. Often, the tuning is done on a simulation model before implementing the control strategy on the actual process. Also, many advanced strategies use model-based control, that is, controllers with a built-in model of the process.
This approach is best illustrated by way of example. Because many important concepts, such as control instrumentation diagrams and control block diagrams, are introduced in the next examples, it is important that you study them thoroughly.
Example 1.1: Liquid Surge Tank
Surge tanks are often used as intermediate storage for fluid streams being transferred between process units. Consider the process flow diagram shown in Figure 1–3, where a fluid stream from process 1 is fed to the surge tank; the effluent from the surge tank is sent to process 2.
)
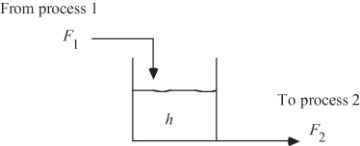
Figure 1–3 Tank level problem
There are obvious constraints on the height in this tank. If the tank overflows, it may create safety and environmental hazards, which may also have economic significance. Let us analyze this system using a step-by-step procedure.
Control objective: The control objective is to maintain the height within certain bounds. If it is too high, it will overflow, and if it is too low, problems with the flow to process 2 may occur. Usually, a specific desired height will be selected. This desired height is known as the setpoint.
Input variables: The input variables are the flow from process 1 and the flow to process 2. Notice that an outlet flow rate is considered an input to this system. The question is, which input is manipulated and which is a disturbance? That depends. We discuss this problem further in a moment.
Output variables: The most important output variable is the liquid level. We assume that it is measured.
Constraints: A number of constraints exist in this problem. There is a maximum liquid level; if it is exceeded, the tank will overflow. There are minimum and maximum flow rates through the inlet and outlet valves.
Operating characteristics: We assume that this is a continuous process, that is, that there is a continuous flow in and out of the tank. It would be a semicontinuous process if, for example, there was an inlet flow with no outlet flow (if the tank was simply being filled).
Safety, environmental, and economic considerations: These aspects depend somewhat on the fluid characteristics. If it is a hazardous chemical, then there is a tremendous incentive from safety and environmental considerations to not allow the tank to overflow. Indeed, this is also an economic consideration, because injuries to employees or environmental cleanup costs money. Even if the substance is water, it has likely been treated by an upstream process unit, so losing water owing to overflow will incur an economic penalty.
Safety considerations play an important role in the specification of control valves (fail-open or fail-closed). For this particular problem, the control-valve specification will depend on which input is manipulated. This is discussed in detail shortly.
Control structure: There are numerous possibilities for control of this system. We discuss first the feedback strategies, then the feedforward strategies.
Feedback Control
The measured variable for a feedback control strategy is the tank height. Which input variable is manipulated depends on what is happening in process 1 and process 2. Let us consider two different scenarios. In scenario 1, process 2 regulates the flow rate 
, leaving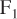 
to be manipulated by a controller. In scenario 2, process 1 regulates the flow rate 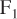, leaving 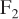to be manipulated by a controller. Here we further discuss scenario 2; scenario 1 is used as a student exercise (exercise 5).
Scenario 2
Process 1 regulates flow rate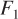 
. This could happen, for example, if process 1 is producing a chemical compound that must be processed by process 2. Perhaps process 1 is set to produce 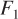at a certain rate. 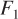is then considered “wild” (a disturbance) by the tank process. In this case, we would adjust 
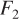to maintain the tank height. Notice that the control valve should be specified as fail-open or air-to-close so that the tank will not overflow on loss of instrument air or other valve failure.
The control and instrumentation diagram for a feedback control strategy for this scenario is shown in Figure 1–4a. Notice that the level transmitter (LT) sends the measured height of liquid in the tank (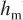
) to the level controller (LC). The LC compares the measured level with the desired level (
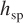, the height setpoint) and sends a pressure signal (
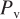) to the valve. This valve top pressure moves the valve stem up and down, changing the flow rate through the valve (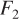). If the controller is designed properly, the flow rate changes to bring the tank height close to the desired setpoint. In this process and instrumentation diagram, we use dashed lines to indicate signals between different pieces of instrumentation.
)
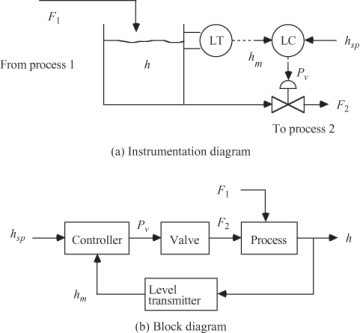
Figure 1–4 Instrumentation and control block diagrams for the tank level feedback control problem. The outlet flow rate (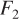) is manipulated, the inlet flow rate (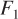) is a disturbance, and the tank height (h) is measured and controlled.
A simplified block diagram representing this system is shown in Figure 1–4b. Each signal and device (or process) is shown on the block diagram. We use a slightly different form for block diagrams when we use transfer function notation for control system analysis in Chapter 5, “Empirical and Discrete-Time Models.” Note that each block represents a dynamic element. We expect that the valve and LT dynamics will be much faster than the process dynamics. We also see clearly from the block diagram why this is known as a feedback control “loop.” The controller “decides” on the valve position, which affects the outlet flow rate (the manipulated input), which affects the level; the inlet flow rate (the disturbance input) also affects the level. The level is measured, and that value is fed back to the controller (which compares the measured level with the desired level [setpoint]).
Feedforward Control
The previous feedback control strategy was based on measuring the output (tank height) and manipulating an input (the outlet flow rate). In this case, the manipulated variable is changed after a disturbance affects the output. The advantage of a feedforward control strategy is that a disturbance variable is measured and a manipulated variable is changed before the output is affected. Consider the preceding case where the inlet flow rate can be changed by the upstream process unit and is therefore considered a disturbance variable. If we can measure the inlet flow rate, we can manipulate the outlet flow rate to maintain a constant tank height. This feedforward control strategy is shown in Figure 1–5a, where FM is the flow measurement device and FFC is the feedforward controller. The corresponding control block diagram is shown in Figure 1–5b. 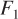is a disturbance input that directly affects the tank height; the value of 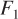is measured by the FM device, and the information is used by an FFC to change the manipulated input, .
)
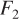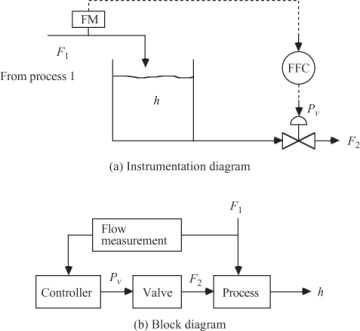
Figure 1–5 Instrumentation and control block diagrams for the tank level feedforward control problem. The inlet flow rate is measured and outlet flow rate is manipulated.
The main disadvantage to this approach is sensitivity to uncertainty. If the inlet flow rate is not perfectly measured or if the outlet flow rate cannot be manipulated perfectly, then the tank height will not be perfectly controlled. With any small disturbance or uncertainty, the tank will eventually overflow or run dry. In practice, FFC is combined with feedback control to account for uncertainty. A feedforward/feedback strategy is shown in Figure 1–6a, and the corresponding block diagram is shown in Figure 1–6b. Here, the feedforward portion allows immediate corrective action to be taken before the disturbance (inlet flow rate) actually affects the output measurement (tank height). The feedback controller adjusts the outlet flow rate to maintain the desired tank height, even with errors in the inlet flow-rate measurement.
)
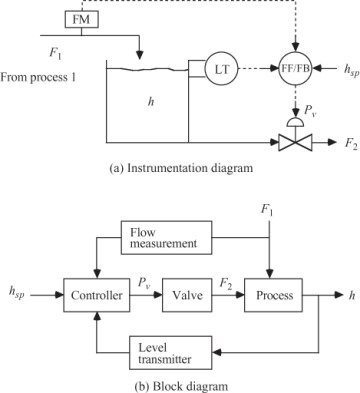
Figure 1–6 Feedforward/feedback control of tank level. The inlet flow rate is the measured disturbance, tank height is the measured output, and outlet flow rate is the manipulated input.
Discussion of Level Controller Tuning and the Dominant Timescale
Notice that we have not discussed the actual control algorithms; the details of control algorithms and tuning are delayed until Chapter 6. Conceptually, would you prefer to tune level controllers for fast or slow responses?
When tanks are used as surge vessels, it is usually desirable to tune the controllers for a slow return to the setpoint. This is particularly true for scenario 2, where the inlet flow rate is considered a disturbance variable. The outlet flow rate is manipulated but affects another process. To avoid upsetting the downstream process, we would like to change the outlet flow rate slowly yet fast enough that the tank does not overflow or go dry.
Related to the controller tuning issue is the importance of the dominant timescale of the process. Consider the case where the maximum tank volume is 200 gallons and the steady-state operating volume is 100 gallons. If the steady-state flow rate is 100 gallons/minute, the residence time would be 1 minute. Assume the inlet flow rate is a disturbance and outlet flow rate is manipulated. If the feed flow rate increased to 150 gallons/minute and the outlet flow rate did not change, the tank would overflow in 2 minutes. On the other hand, if the same vessel had a steady-state flow rate of 10 gallons/minute and the inlet flow suddenly increased to 15 gallons/minute (with no change in the outlet flow), it would take 20 minutes for the tank to overflow. Clearly, controller tuning and concern about controller failure are different for these two cases.
The first example was fairly easy compared with most control-system synthesis problems in industry. Even for this simple example, we found that many issues must be considered and a number of decisions (specification of a fail-open or fail-closed valve, etc.) must be made. Often, there are many (and usually conflicting) objectives, many possible manipulated variables, and numerous possible measured variables.
It is helpful to think of common, everyday activities in the context of control to familiarize yourself with the types of control problems that can arise in practice. Examples include taking a shower (which is analyzed in the supplemental material) and driving a car. It is suggested that you work through such examples provided in Exericse 1 in the Student Exercises section of this chapter.
Examples of control loops abound in nature, and particularly in physiological systems. The human body regulates many variables through homeostasis; examples include temperature, blood pressure, and blood glucose—which is the topic of the next example.
Example 1.2: Glucose Regulation by the Pancreas
The primary energy source for the human body is glucose, so it is important that the human body be able to regulate the blood glucose concentration. The basic mechanisms for blood glucose regulation are shown in Figure 1–7. If the blood glucose is high, due to a recently consumed meal, for example, then the beta cells of the pancreas are activated to produce insulin. The insulin then stimulates the uptake of glucose from the blood into the cells for maintenance and growth and the conversion of glucose into glycogen in the liver, thus lowering the blood glucose. If the blood glucose is low, the alpha cells of the pancreas promote the conversion of glycogen back into glucose in the liver, thus raising the blood glucose.
)
Figure 1–7 Blood glucose regulation by the pancreas. Source: Craig Freudenrich, “How Diabetes Works,” http://science.howstuffworks.com/life/human-biology/diabetes1.htm.
Here we analyze this glucose regulatory system in the context of a control problem:
Control objective: The control objective is to maintain the desired glucose level, or setpoint.
Input variables: One manipulated input variable is the production of insulin by the beta cells; another manipulated input is the production of glucagon by the alpha cells. A number of disturbance inputs affect blood glucose, including meals (that tend to raise glucose) and exercise; aerobic exercise decreases glucose, whereas vigorous anaerobic exercise can briefly increase the glucose level.
Output variables: The key output variable is blood glucose concentration.
Constraints: There are possibly a number of constraints in this problem. The insulin and glucagon values cannot go below zero, and there are maximum rates on their values (as well as their rates of change); these are likely hard constraints that may be time-dependent. Soft constraints include lower and upper bounds on the blood glucose concentration, as discussed further in the safety analysis.
Operating characteristics: This is a continuous process, with discrete events such as meals and exercise.
Safety, environmental, and economic considerations: A too low blood glucose level (known as hypoglycemia) has short-term effects, including possible dizziness, while high blood glucose for an extended period of time has long-term health consequences, including retinal diseases.
Control structure: In play are numerous control actions because many hormones have a role in blood glucose regulation. The diagram primarily describes feedback control because insulin and glucagon rates are changed once there is a glucose change; as a side note, this two-input strategy is similar to split-range control, which is covered in Chapter 12, “Ratio, Selective, and Split-Range Control.” Not discussed in the diagram are feedforward strategies—for example, the salivation that occurs when eating is anticipated may actually prime the beta cells for insulin production before the blood glucose actually changes.
The glucose regulatory system is disrupted if an individual has diabetes, of which there are two primary forms: type 1 and type 2. Roughly 5% to 10% of people with diabetes have type 1, which was formerly known as juvenile diabetes. In type 1 diabetes, most of the beta cells of the pancreas cease to produce insulin. Thus, an individual with type 1 diabetes must take insulin subcutaneously—either with multiple daily injections of insulin or with a continuous insulin infusion pump. As shown in examples in this textbook, an automated insulin delivery system (closed-loop artificial pancreas) consists of a glucose sensor, insulin infusion pump, and control algorithm (usually on a wearable microprocessor, such as a smartphone) to automatically adjust insulin delivery rates based on the glucose signal (see Figure 1–8). In an individual with type 2 diabetes, the pancreas still produces insulin, but either the amount is insufficient or the individual is insulin resistant (does not respond effectively to insulin). Usual interventions include oral medications and changes in diet and exercise, although an increasing number of people with type 2 diabetes use insulin and check their blood glucose.
)
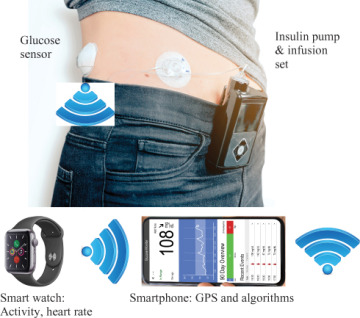
Figure 1–8 An automated insulin delivery system. The glucose sensor sends a signal to the smartphone, which calculates the next insulin delivery rate and sends a signal to the insulin pump, leading to changes in the blood glucose concentration. In addition, the smart watch provides feedforward information about exercise to the smart phone.
(Photo: Carlo Prearo/Shutterstock; smart phone monitor: Andrey_Popov/Shutterstock; smart watch: WakoPako/Shutterstock; wifi icon: iconmonstr/Shutterstock)
So far, this chapter has covered the important first step of control system development, identifying seven basic steps in analyzing a process control problem. We have used simple examples with which you are familiar. As you learn about more chemical, biological, and environmental processes, you should get in the habit of thinking about them from a process systems point of view, just as you have with these simple systems.